Description of Book Knot Simplifier

by
Maria Andreeva, Ivan Dynnikov, Sergey Koval, Konrad Polthier, Iskander Taimanov

Here we offer a set of tools for manipulating knots and links in the three-space by using the three-page presentation of links, which was proposed and developed by I. Dynnikov in [1][2][3].

The approach is based on a simple and very well known observation that every link in the three-space is topologically equivalent to a link that lies entirely in a three-page book, i.e. the union of three half-planes with common boundary. Though being not convenient for human perception, this way of presenting links seems to be very efficient for handling knots by computer. It provides a very quick way from a combinatorial description of a link to its three-dimensional presentation. A three-page link admits a lot of transformations that preserve its isotopy class and can be easily found. This fact is used in the knot simplifying tool included herein.

This software for knot manipulation and simplification builds on the JavaView library [5].

Currently available ...

View a knot available on the server

Input your own knot as a 3D curve or a Gauss code

Simplify a knot

Edit a knot

Tools being developed ...

More editing tools

Converting to/from other formats

Comparing and recognizing knots

View a knot

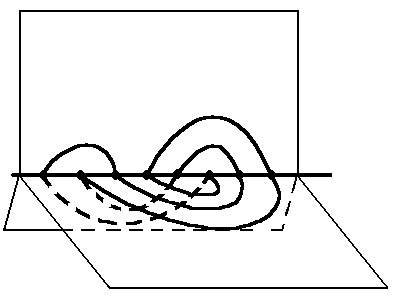
To download a knot from the server click "Choose knot" button. At the present time, we have a collection of knots presented in .jkb format, as 3D curve (.txt files), and as a Gauss code (.gc files).

Files 31.jkb, 141.jkb, 322.jkb, and 539  have been generated automatically from hand-made (ID) planar diagrams of unknots having 31, 141, 322, and 539 crossings respectively. These unknots were used to test the simplifier. The unknot with 31 crossings is shown below.

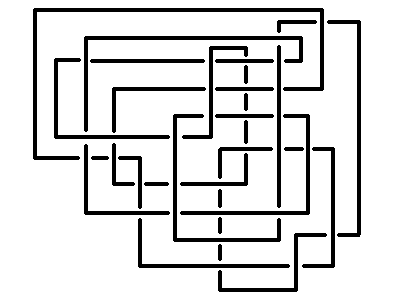
The unknot with 539 crossings is a satellite of this unknot (see [1] for a picture).

The source of the knots in TXT format is the Knot-Plot web site created by Robert Scharein [4] which contains a collection of knots and links with small crossing number (less than or equal to 10). The files with .gc extension contain Gauss codes of the same links. These codes were generated automatically (SK) from the .txt files.

For converting a planar diagram to a three-page diagram the algorithm described in [1] is used.

Input a knot

To input your own knot click "Input knot" button and choose a method of input. Now available methods are by using 3D curve or the Gauss code. If you are already using some other knot presentation with another software, you are welcome to let us know the specification of the format you are using by sending e-mail at dynnikov@mech.math.msu.su. Then, we may make it possible to input a knot in your favorite format.

Simplify a knot

If you press the "Simplify" button, the knot simplifier starts. It implements an algorithm described in [1]. We shall explain very shortly the idea of the algorithm.

In the case of the three-page presentation of knots, a natural measure of complexity is the number of intersection points of the knot with the binding line of the three-page book. The simplifier performs operations on the knot that preserve the isotopy class of the knot and tries to make the complexity as less as possible. Let us consider how this works. Look at the following three-page knot, which is the trefoil knot in fact.

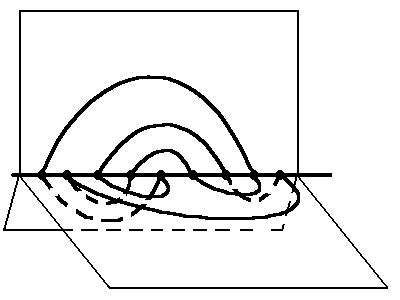
Its complexity equals 9. What if we replace the part of the knot marked in red with the curve marked in blue in the figure below?

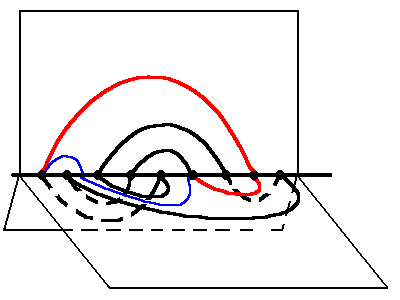
We obtain a topologically equivalent knot of the same complexity, but now we obviously can simplify it by contracting the arc connecting the two rightmost points:

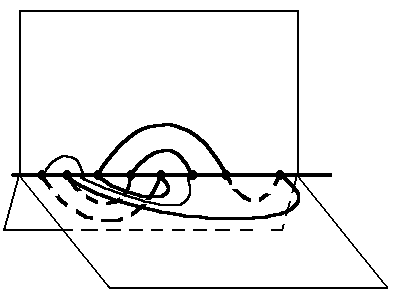
After doing that, we obtain a three-page knot of complexity 8.

The knot simplifier just tries to simplify a given knot by transformations of this kind. If sufficiently many subsequent trials are not successful, i.e. the knot is not simplified for a long time, the simplifier stops. More details about the transformations used in the simplifier see [1].

At the present state, the simplifier does not search among all three-page diagrams that can be obtain from the current one by available transforms and does not make a "canonical" choice. So, if you click the "Simplify" button again, the picture may change.

Edit a knot

The only available editing tool for now is cyclic permutation of vertices on the binding line, which is achieved by pressing the "Vertex permutation" button. Other editing tools coming soon.

Input a knot as a 3D curve

To input a knot presented by a 3D polygon just type coordinates of all vertices in the order they follow on the knot. Coordinates must be separated by blank spaces or new lines.
For example the trefoil knot is presented by a polygon with vertices (0,0,0), (3,0,1), (0,2,0), (1,0,1), (0,4,0), (4,0,1), (0,1,0), (2,0,1), (0,3,0), (0,0,1). To input it, type
0 0 0 3 0 1 0 2 0 1 0 1 0 4 0 4 0 1 0 1 0 2 0 1 0 3 0 0 0 1
and click "ok" button. The Gauss code of the knot appears. Click "ok" button again to see the three-page picture of the knot.

If your link consists of more than one connected component, separate records for different components by a blank line.

Warning: at the present state, for converting a 3D polygon to a planar diagram of a knot, projection along the z-axis is used. If the projection of your knot along the z-axis is not generic (i.e. two vertices are projected to the same point, a vertex is projected to an internal point of an edge, or a triple crossing occurs), then the conversion may fail.
 

Input the Gauss code of a knot

If you have planar diagram of a knot or link you may input it by typing its Gauss code. The diagram must be connected and have at least one crossing. We use an encoding a little different from what is usually called Gauss code, providing additional information that allows to distinguish knots from their mirror images. To input the link do the following.

For each component, choose an orientation and a starting point.

Assign different indices, which must be natural numbers, to all the crossings.

For each connected component, go along it starting from the marked point in the chosen direction, and each time you come through a crossing, write down the index of the crossing preceded by two symbols: the first one must be + or - indicating whether you go over or under the crossing, and the second must be  >  or  <  sign indicating whether you see the arc that you intersect going from left two the right or from right to the left, respectively. Entries for different crossings must be separated by spaces.

When you come back to the starting point of the chosen component, proceed with the next one. Separate entries for different components by keyword "component".

For example, for the diagram below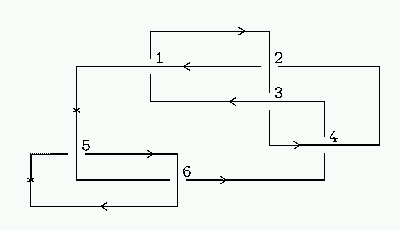

you get the following Gauss code:
->5 +<6  component  +<5 ->6 ->4 +<3 -<1 +>2 ->3 +<4 -<2 +>1

This way of inputting links seems to take much time. We are now working on a better format for input.

Description of the .jkb format

Still has to be written...

Editing tools being developed

Adding/removing vertices/arcs, coloring components, taking connected sum, and more.

Converting to/from other formats

In order to make the package more convenient for those who want to use it in their own research  we are going to provide converters to and from all popular formats for presenting knots. In particular, it will be possible to input a knot as a closure of a braid or a tangle word. If you are already using some format for presenting knots, please, send the specification of the format at dynnikov@mech.math.msu.su

References

[1] I. A. Dynnikov. Three-page link presentation and an untangling algorithm.
Proc. of the International Conference Low-Dimensional Topology and Combinatorial Group Theory,
Chelyabinsk, July, 31 - August 7, 1999; Kiev, 2000; pp. 112--130.

[2] I. A. Dynnikov. Three-page approach to knot theory. Universal semigroup. (Russian) Funktsional'nyi Analiz i Ego Prilozhenija, 34 (2000), no. 1, 29--40; translation in Functional Analysis and Its Appl. 34 (2000), no. 1, 24--32.

[3] I. A. Dynnikov. Three-page approach to knot theory. Encoding and local moves. (Russian)
Funktsional'nyi Analiz i Ego Prilozhenija, 33 (1999), no. 4, 25--37; translation in Functional Analysis and Its Appl. 33 (1999), no. 4, 260--269. MR 2000m:57007

[4] Robert Scharein Knot-Plot Homepage at http://www.pims.math.ca/knotplot.

[5] JavaView Homepage at http://www.javaview.de.